
I LOVE teaching Order of Operations. Students are usually overwhelmed by the topic at first. However, once they get the hang of it, they love it too! However, there are many common order of operations mistakes that students tend to make.
Are you looking for more ideas to mix up your math lessons and engage your students? Check out my FREE Guide to an Engaging Math Lesson! It has tons of ideas for creating variety in your math lessons while keeping your students engaged and learning!
Common Order of Operations Mistakes Students Make
Working ONLY Left to Right
Students are DYING to work from left to right, no matter what. If you think about it, this makes sense. This is how we all read and these kiddos are young. They have been forcing their brains to work left to right for the past 4-5 years. Now, we are asking them to look at math problems in a whole new way! In order to break this habit, it is important to explicitly teach students the rules to avoid this mistake.
Two commonly used acronyms are PEMDAS and GEMS. It is critical to explicitly explain what the rules mean and demonstrate using multiple examples. When I first started teaching, I made the mistake of thinking that just teaching the rules would be enough. It turns out that there will always be several students that don’t understand that the list is actually giving an ORDER of operations.
I know, it seems a bit ridiculous to us math teachers, but kids just don’t always “get it” on the first try with this one. One way I help kids understand is by actually having them write First, Second, Third, Fourth next to the acronym as we learn it, like in this notebook page:

I also make sure that my students build up to larger problems slowly. I like using this domino game in my classroom either as partner work or in centers so that students get the practice they need with smaller expressions before moving on to longer, more complicated ones.
Always Multiplying or Adding First
The next common mistake is wanting to do one operation before another. Remember, we now WANT them to work left to right when doing multiplication/division or addition/subtraction. This can be infinitely frustrating for the students. It is important to not just teach students to memorize Multiplication, Division, Addition, Subtraction, but that we teach them to memorize these phrases: “multiplication division left to right,” “addition subtraction left to right.”
To help this stick, I make a big deal of saying each phrase in a way that sticks in their minds. I might say each phrase in a silly voice or really fast. Also, this is a part of what we write in our notes and what goes up on my anchor chart.
Double-using Numbers
When students are solving a portion of the problem, at times they may bring down a number they just used into the next part of the problem. Here is an example:

In the example, the student used the 3 twice. Then, he didn’t know what to do next. At this point, students may guess or even combine the numbers into one long number. To combat this problem, I have students cross off any numbers and operations they solve. Then we write the solution to that part of the problem. Finally, we re-copy any portions of the problem they have not yet used like this:
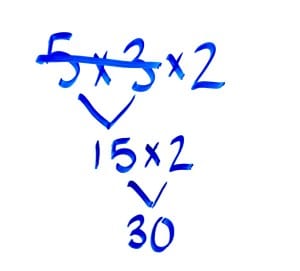
Not Following the Order of Operations Within Parentheses
Since we teach students to solve the parts of the problem within parentheses first, when there are multiple operations within those parentheses, we will often see students reverting back to doing everything left to right. It is important to teach them that the multiplication/division and addition/subtraction rules still apply inside parentheses. This is yet another rule that needs to be taught explicitly. Do not assume that your students will just automatically apply the rule within the parentheses.
Multiplying the Base by the Exponent
In this common order of operations mistake, students will multiply the base number by the exponent (instead of by itself). If you are using exponents in your order of operations problems, be sure that the students have a full grasp of exponents in isolation before they move onto this topic.
Not Re-Writing all Parts of the Problem Correctly
Students have the most difficulty with this as they work through problems with the nested grouping symbols. They will solve one portion of the problem and then as they copy the problem to the next layer, they will incorrectly transcribe the problem from the line before.
I most often see them omitting the grouping symbols. This completely changes the meaning of the problem. In my experience, this happens most often when students are rushing. I try to make sure that students work through their order of operations as slowly as necessary, and I even let some students check their work after each question for accuracy. I also like to give my students a variety of questions with nesting symbols in them so they get plenty of practice. This set of task cards is perfect for making sure the students get the practice they need.
Do you see other common mistakes in your class, or have other things you do to overcome mistakes? Comment below to share!
AND! Don’t forget to download your FREE Guide to an Engaging Math Lesson today!
Happy teaching,




